October 22, 2024

The Inclusion-Exclusion Principle¶

The inclusion-exclusion principle is an important combinatorial way to compute the size of a set or the probability of complex events. It relates the sizes of individual sets with their union.

Statement¶

The verbal formula¶

The inclusion-exclusion principle can be expressed as follows:

To compute the size of a union of multiple sets, it is necessary to sum the sizes of these sets separately, and then subtract the sizes of all pairwise intersections of the sets, then add back the size of the intersections of triples of the sets, subtract the size of quadruples of the sets, and so on, up to the intersection of all sets.

The formulation in terms of sets¶

The above definition can be expressed mathematically as follows:

| ⋃_{i = 1}^{n} A_{i} | = \sum_{i = 1}^{n} | A_{i} | - \sum_{1 \leq i < j \leq n} | A_{i} \cap A_{j} | + \sum_{1 \leq i < j < k \leq n} | A_{i} \cap A_{j} \cap A_{k} | - \dots + (- 1)^{n - 1} | A_{1} \cap \dots \cap A_{n} |

And in a more compact way:

| ⋃_{i = 1}^{n} A_{i} | = \sum_{\emptyset \neq J \subseteq {1, 2, \dots, n}} (- 1)^{| J | - 1} | ⋂_{j \in J} A_{j} |

The formulation using Venn diagrams¶

Let the diagram show three sets $A$ , $B$ and $C$ :

Venn diagram

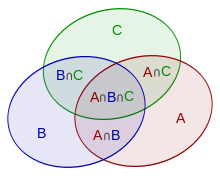
Then the area of their union $A \cup B \cup C$ is equal to the sum of the areas $A$ , $B$ and $C$ less double-covered areas $A \cap B$ , $A \cap C$ , $B \cap C$ , but with the addition of the area covered by three sets $A \cap B \cap C$ :

S (A \cup B \cup C) = S (A) + S (B) + S (C) - S (A \cap B) - S (A \cap C) - S (B \cap C) + S (A \cap B \cap C)

It can also be generalized for an association of $n$ sets.

The formulation in terms of probability theory¶

If $A_{i}$ $(i = 1, 2. . . n)$ are events and $P (A_{i})$ the probability of an event from $A_{i}$ to occur, then the probability of their union (i.e. the probability that at least one of the events occur) is equal to:

\begin{array}{rcl} P (⋃_{i = 1}^{n} A_{i}) & = & \sum_{i = 1}^{n} P (A_{i}) - \sum_{1 \leq i < j \leq n} P (A_{i} \cap A_{j}) + \\ + & \sum_{1 \leq i < j < k \leq n} P (A_{i} \cap A_{j} \cap A_{k}) - \dots + (- 1)^{n - 1} P (A_{1} \cap \dots \cap A_{n}) \end{array}

And in a more compact way:

P (⋃_{i = 1}^{n} A_{i}) = \sum_{\emptyset \neq J \subseteq {1, 2, \dots, n}} (- 1)^{| J | - 1} P (⋂_{j \in J} A_{j})

Proof¶

For the proof it is convenient to use the mathematical formulation in terms of set theory:

| ⋃_{i = 1}^{n} A_{i} | = \sum_{\emptyset \neq J \subseteq {1, 2, \dots, n}} (- 1)^{| J | - 1} | ⋂_{j \in J} A_{j} |

We want to prove that any element contained in at least one of the sets $A_{i}$ will occur in the formula only once (note that elements which are not present in any of the sets $A_{i}$ will never be considered on the right part of the formula).

Consider an element $x$ occurring in $k \geq 1$ sets $A_{i}$ . We will show it is counted only once in the formula. Note that:

in terms which $| J | = 1$ , the item $x$ will be counted $+ k$ times;
in terms which $| J | = 2$ , the item $x$ will be counted $- (\binom{k}{2})$ times - because it will be counted in those terms that include two of the $k$ sets containing $x$ ;
in terms which $| J | = 3$ , the item $x$ will be counted $+ (\binom{k}{3})$ times;
$\dots$
in terms which $| J | = k$ , the item $x$ will be counted $(- 1)^{k - 1} \cdot (\binom{k}{k})$ times;
in terms which $| J | > k$ , the item $x$ will be counted zero times;

This leads us to the following sum of binomial coefficients:

T = (\binom{k}{1}) - (\binom{k}{2}) + (\binom{k}{3}) - \dots + (- 1)^{i - 1} \cdot (\binom{k}{i}) + \dots + (- 1)^{k - 1} \cdot (\binom{k}{k})

This expression is very similar to the binomial expansion of $(1 - x)^{k}$ :

(1 - x)^{k} = (\binom{k}{0}) - (\binom{k}{1}) \cdot x + (\binom{k}{2}) \cdot x^{2} - (\binom{k}{3}) \cdot x^{3} + \dots + (- 1)^{k} \cdot (\binom{k}{k}) \cdot x^{k}

When $x = 1$ , $(1 - x)^{k}$ looks a lot like $T$ . However, the expression has an additional $(\binom{k}{0}) = 1$ , and it is multiplied by $- 1$ . That leads us to $(1 - 1)^{k} = 1 - T$ . Therefore $T = 1 - (1 - 1)^{k} = 1$ , what was required to prove. The element is counted only once.

Generalization for calculating number of elements in exactly $r$ sets¶

Inclusion-exclusion principle can be rewritten to calculate number of elements which are present in zero sets:

| ⋂_{i = 1}^{n} \overset{―}{A_{i}} | = \sum_{m = 0}^{n} (- 1)^{m} \sum_{| X | = m} | ⋂_{i \in X} A_{i} |

Consider its generalization to calculate number of elements which are present in exactly $r$ sets:

| ⋃_{| B | = r} [⋂_{i \in B} A_{i} \cap ⋂_{j \notin B} \overset{―}{A_{j}}] | = \sum_{m = r}^{n} (- 1)^{m - r} (\binom{m}{r}) \sum_{| X | = m} | ⋂_{i \in X} A_{i} |

To prove this formula, consider some particular $B$ . Due to basic inclusion-exclusion principle we can say about it that:

| ⋂_{i \in B} A_{i} \cap ⋂_{j \notin B} \overset{―}{A_{j}} | = \sum_{m = r}^{n} (- 1)^{m - r} \sum_{\begin{matrix} | X | = m \\ B \subset X \end{matrix}} | ⋂_{i \in X} A_{i} |

The sets on the left side do not intersect for different $B$ , thus we can sum them up directly. Also one should note that any set $X$ will always have coefficient $(- 1)^{m - r}$ if it occurs and it will occur for exactly $(\binom{m}{r})$ sets $B$ .

Usage when solving problems¶

The inclusion-exclusion principle is hard to understand without studying its applications.

First, we will look at three simplest tasks "at paper", illustrating applications of the principle, and then consider more practical problems which are difficult to solve without inclusion-exclusion principle.

Tasks asking to "find the number of ways" are worth of note, as they sometimes lead to polynomial solutions, not necessarily exponential.

A simple task on permutations¶

Task: count how many permutations of numbers from $0$ to $9$ exist such that the first element is greater than $1$ and the last one is less than $8$ .

Let's count the number of "bad" permutations, that is, permutations in which the first element is $\leq 1$ and/or the last is $\geq 8$ .

We will denote by $X$ the set of permutations in which the first element is $\leq 1$ and $Y$ the set of permutations in which the last element is $\geq 8$ . Then the number of "bad" permutations, as on the inclusion-exclusion formula, will be:

| X \cup Y | = | X | + | Y | - | X \cap Y |

After a simple combinatorial calculation, we will get to:

2 \cdot 9! + 2 \cdot 9! - 2 \cdot 2 \cdot 8!

The only thing left is to subtract this number from the total of $10!$ to get the number of "good" permutations.

A simple task on (0, 1, 2) sequences¶

Task: count how many sequences of length $n$ exist consisting only of numbers $0, 1, 2$ such that each number occurs at least once.

Again let us turn to the inverse problem, i.e. we calculate the number of sequences which do not contain at least one of the numbers.

Let's denote by $A_{i} (i = 0, 1, 2)$ the set of sequences in which the digit $i$ does not occur. The formula of inclusion-exclusion on the number of "bad" sequences will be:

| A_{0} \cup A_{1} \cup A_{2} | = | A_{0} | + | A_{1} | + | A_{2} | - | A_{0} \cap A_{1} | - | A_{0} \cap A_{2} | - | A_{1} \cap A_{2} | + | A_{0} \cap A_{1} \cap A_{2} |

The size of each $A_{i}$ is $2^{n}$ , as each sequence can only contain two of the digits.
The size of each pairwise intersection $A_{i} \cap A_{j}$ is equal to $1$ , as there will be only one digit to build the sequence.
The size of the intersection of all three sets is equal to $0$ , as there will be no digits to build the sequence.

As we solved the inverse problem, we subtract it from the total of $3^{n}$ sequences:

3^{n} - (3 \cdot 2^{n} - 3 \cdot 1 + 0)

Number of upper-bound integer sums¶

Consider the following equation:

x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + x_{6} = 20

where $0 \leq x_{i} \leq 8 (i = 1, 2, \dots 6)$ .

Task: count the number of solutions to the equation.

Forget the restriction on $x_{i}$ for a moment and just count the number of nonnegative solutions to this equation. This is easily done using Stars and Bars: we want to break a sequence of $20$ units into $6$ groups, which is the same as arranging $5$ bars and $20$ stars:

N_{0} = (\binom{25}{5})

We will now calculate the number of "bad" solutions with the inclusion-exclusion principle. The "bad" solutions will be those in which one or more $x_{i}$ are greater than or equal to $9$ .

Denote by $A_{k} (k = 1, 2 \dots 6)$ the set of solutions where $x_{k} \geq 9$ , and all other $x_{i} \geq 0 (i \neq k)$ (they may be $\geq 9$ or not). To calculate the size of $A_{k}$ , note that we have essentially the same combinatorial problem that was solved in the two paragraphs above, but now $9$ of the units are excluded from the slots and definitely belong to the first group. Thus:

| A_{k} | = (\binom{16}{5})

Similarly, the size of the intersection between two sets $A_{k}$ and $A_{p}$ (for $k \neq p$ ) is equal to:

| A_{k} \cap A_{p} | = (\binom{7}{5})

The size of each intersection of three sets is zero, since $20$ units will not be enough for three or more variables greater than or equal to $9$ .

Combining all this into the formula of inclusions-exceptions and given that we solved the inverse problem, we finally get the answer:

(\binom{25}{5}) - ((\binom{6}{1}) \cdot (\binom{16}{5}) - (\binom{6}{2}) \cdot (\binom{7}{5}))

This easily generalizes to $d$ numbers that sum up to $s$ with the restriction $0 \leq x_{i} \leq b$ :

\sum_{i = 0}^{d} (- 1)^{i} (\binom{d}{i}) (\binom{s + d - 1 - (b + 1) i}{d - 1})

As above, we treat binomial coefficients with negative upper index as zero.

Note this problem could also be solved with dynamic programming or generating functions. The inclusion-exclusion answer is computed in $O (d)$ time (assuming math operations like binomial coefficient are constant time), while a simple DP approach would take $O (d s)$ time.

The number of relative primes in a given interval¶

Task: given two numbers $n$ and $r$ , count the number of integers in the interval $[1; r]$ that are relatively prime to n (their greatest common divisor is $1$ ).

Let's solve the inverse problem - compute the number of not mutually primes with $n$ .

We will denote the prime factors of $n$ as $p_{i} (i = 1 \dots k)$ .

How many numbers in the interval $[1; r]$ are divisible by $p_{i}$ ? The answer to this question is:

⌊ \frac{r}{p_{i}} ⌋

However, if we simply sum these numbers, some numbers will be summarized several times (those that share multiple $p_{i}$ as their factors). Therefore, it is necessary to use the inclusion-exclusion principle.

We will iterate over all $2^{k}$ subsets of $p_{i}$ s, calculate their product and add or subtract the number of multiples of their product.

Here is a C++ implementation:

int solve (int n, int r) {
    vector<int> p;
    for (int i=2; i*i<=n; ++i)
        if (n % i == 0) {
            p.push_back (i);
            while (n % i == 0)
                n /= i;
        }
    if (n > 1)
        p.push_back (n);

    int sum = 0;
    for (int msk=1; msk<(1<<p.size()); ++msk) {
        int mult = 1,
            bits = 0;
        for (int i=0; i<(int)p.size(); ++i)
            if (msk & (1<<i)) {
                ++bits;
                mult *= p[i];
            }

        int cur = r / mult;
        if (bits % 2 == 1)
            sum += cur;
        else
            sum -= cur;
    }

    return r - sum;
}

Asymptotics of the solution is $O (\sqrt{n})$ .

The number of integers in a given interval which are multiple of at least one of the given numbers¶

Given $n$ numbers $a_{i}$ and number $r$ . You want to count the number of integers in the interval $[1; r]$ that are multiple of at least one of the $a_{i}$ .

The solution algorithm is almost identical to the one for previous task — construct the formula of inclusion-exclusion on the numbers $a_{i}$ , i.e. each term in this formula is the number of numbers divisible by a given subset of numbers $a_{i}$ (in other words, divisible by their least common multiple).

So we will now iterate over all $2^{n}$ subsets of integers $a_{i}$ with $O (n \log r)$ operations to find their least common multiple, adding or subtracting the number of multiples of it in the interval. Asymptotics is $O (2^{n} \cdot n \cdot \log r)$ .

The number of strings that satisfy a given pattern¶

Consider $n$ patterns of strings of the same length, consisting only of letters ( $a . . . z$ ) or question marks. You're also given a number $k$ . A string matches a pattern if it has the same length as the pattern, and at each position, either the corresponding characters are equal or the character in the pattern is a question mark. The task is to count the number of strings that match exactly $k$ of the patterns (first problem) and at least $k$ of the patterns (second problem).

Notice first that we can easily count the number of strings that satisfy at once all of the specified patterns. To do this, simply "cross" patterns: iterate though the positions ("slots") and look at a position over all patterns. If all patterns have a question mark in this position, the character can be any letter from $a$ to $z$ . Otherwise, the character of this position is uniquely defined by the patterns that do not contain a question mark.

Learn now to solve the first version of the problem: when the string must satisfy exactly $k$ of the patterns.

To solve it, iterate and fix a specific subset $X$ from the set of patterns consisting of $k$ patterns. Then we have to count the number of strings that satisfy this set of patterns, and only matches it, that is, they don't match any other pattern. We will use the inclusion-exclusion principle in a slightly different manner: we sum on all supersets $Y$ (subsets from the original set of strings that contain $X$ ), and either add to the current answer or subtract it from the number of strings:

a n s (X) = \sum_{Y \supseteq X} (- 1)^{| Y | - k} \cdot f (Y)

Where $f (Y)$ is the number of strings that match $Y$ (at least $Y$ ).

(If you have a hard time figuring out this, you can try drawing Venn Diagrams.)

If we sum up on all $a n s (X)$ , we will get the final answer:

a n s = \sum_{X : | X | = k} a n s (X)

However, asymptotics of this solution is $O (3^{k} \cdot k)$ . To improve it, notice that different $a n s (X)$ computations very often share $Y$ sets.

We will reverse the formula of inclusion-exclusion and sum in terms of $Y$ sets. Now it becomes clear that the same set $Y$ would be taken into account in the computation of $a n s (X)$ of $(\binom{| Y |}{k})$ sets with the same sign $(- 1)^{| Y | - k}$ .

a n s = \sum_{Y : | Y | \geq k} (- 1)^{| Y | - k} \cdot (\binom{| Y |}{k}) \cdot f (Y)

Now our solution has asymptotics $O (2^{k} \cdot k)$ .

We will now solve the second version of the problem: find the number of strings that match at least $k$ of the patterns.

Of course, we can just use the solution to the first version of the problem and add the answers for sets with size greater than $k$ . However, you may notice that in this problem, a set |Y| is considered in the formula for all sets with size $\geq k$ which are contained in $Y$ . That said, we can write the part of the expression that is being multiplied by $f (Y)$ as:

(- 1)^{| Y | - k} \cdot (\binom{| Y |}{k}) + (- 1)^{| Y | - k - 1} \cdot (\binom{| Y |}{k + 1}) + (- 1)^{| Y | - k - 2} \cdot (\binom{| Y |}{k + 2}) + \dots + (- 1)^{| Y | - | Y |} \cdot (\binom{| Y |}{| Y |})

Looking at Graham's (Graham, Knuth, Patashnik. "Concrete mathematics" [1998] ), we see a well-known formula for binomial coefficients:

\sum_{k = 0}^{m} (- 1)^{k} \cdot (\binom{n}{k}) = (- 1)^{m} \cdot (\binom{n - 1}{m})

Applying it here, we find that the entire sum of binomial coefficients is minimized:

(- 1)^{| Y | - k} \cdot (\binom{| Y | - 1}{| Y | - k})

Thus, for this task, we also obtained a solution with the asymptotics $O (2^{k} \cdot k)$ :

a n s = \sum_{Y : | Y | \geq k} (- 1)^{| Y | - k} \cdot (\binom{| Y | - 1}{| Y | - k}) \cdot f (Y)

The number of ways of going from a cell to another¶

There is a field $n \times m$ , and $k$ of its cells are impassable walls. A robot is initially at the cell $(1, 1)$ (bottom left). The robot can only move right or up, and eventually it needs to get into the cell $(n, m)$ , avoiding all obstacles. You need to count the number of ways he can do it.

Assume that the sizes $n$ and $m$ are very large (say, $10^{9}$ ), and the number $k$ is small (around $100$ ).

For now, sort the obstacles by their coordinate $x$ , and in case of equality — coordinate $y$ .

Also just learn how to solve a problem without obstacles: i.e. learn how to count the number of ways to get from one cell to another. In one axis, we need to go through $x$ cells, and on the other, $y$ cells. From simple combinatorics, we get a formula using binomial coefficients:

(\binom{x + y}{x})

Now to count the number of ways to get from one cell to another, avoiding all obstacles, you can use inclusion-exclusion to solve the inverse problem: count the number of ways to walk through the board stepping at a subset of obstacles (and subtract it from the total number of ways).

When iterating over a subset of the obstacles that we'll step, to count the number of ways to do this simply multiply the number of all paths from starting cell to the first of the selected obstacles, a first obstacle to the second, and so on, and then add or subtract this number from the answer, in accordance with the standard formula of inclusion-exclusion.

However, this will again be non-polynomial in complexity $O (2^{k} \cdot k)$ .

Here goes a polynomial solution:

We will use dynamic programming. For convenience, push (1,1) to the beginning and (n,m) at the end of the obstacles array. Let's compute the numbers $d [i]$ — the number of ways to get from the starting point ( $0 - t h$ ) to $i - t h$ , without stepping on any other obstacle (except for $i$ , of course). We will compute this number for all the obstacle cells, and also for the ending one.

Let's forget for a second the obstacles and just count the number of paths from cell $0$ to $i$ . We need to consider some "bad" paths, the ones that pass through the obstacles, and subtract them from the total number of ways of going from $0$ to $i$ .

When considering an obstacle $t$ between $0$ and $i$ ( $0 < t < i$ ), on which we can step, we see that the number of paths from $0$ to $i$ that pass through $t$ which have $t$ as the first obstacle between start and $i$ . We can compute that as: $d [t]$ multiplied by the number of arbitrary paths from $t$ to $i$ . We can count the number of "bad" ways summing this for all $t$ between $0$ and $i$ .

We can compute $d [i]$ in $O (k)$ for $O (k)$ obstacles, so this solution has complexity $O (k^{2})$ .

The number of coprime quadruples¶

You're given $n$ numbers: $a_{1}, a_{2}, \dots, a_{n}$ . You are required to count the number of ways to choose four numbers so that their combined greatest common divisor is equal to one.

We will solve the inverse problem — compute the number of "bad" quadruples, i.e. quadruples in which all numbers are divisible by a number $d > 1$ .

We will use the inclusion-exclusion principle while summing over all possible groups of four numbers divisible by a divisor $d$ .

a n s = \sum_{d \geq 2} (- 1)^{d e g (d) - 1} \cdot f (d)

where $d e g (d)$ is the number of primes in the factorization of the number $d$ and $f (d)$ the number of quadruples divisible by $d$ .

To calculate the function $f (d)$ , you just have to count the number of multiples of $d$ (as mentioned on a previous task) and use binomial coefficients to count the number of ways to choose four of them.

Thus, using the formula of inclusions-exclusions we sum the number of groups of four divisible by a prime number, then subtract the number of quadruples which are divisible by the product of two primes, add quadruples divisible by three primes, etc.

The number of harmonic triplets¶

You are given a number $n \leq 10^{6}$ . You are required to count the number of triples $2 \leq a < b < c \leq n$ that satisfy one of the following conditions:

or $g c d (a, b) = g c d (a, c) = g c d (b, c) = 1$ ,
or $g c d (a, b) > 1, g c d (a, c) > 1, g c d (b, c) > 1$ .

First, go straight to the inverse problem — i.e. count the number of non-harmonic triples.

Second, note that any non-harmonic triplet is made of a pair of coprimes and a third number that is not coprime with at least one from the pair.

Thus, the number of non-harmonic triples that contain $i$ is equal the number of integers from $2$ to $n$ that are coprimes with $i$ multiplied by the number of integers that are not coprime with $i$ .

Either $g c d (a, b) = 1 \land g c d (a, c) > 1 \land g c d (b, c) > 1$

or $g c d (a, b) = 1 \land g c d (a, c) = 1 \land g c d (b, c) > 1$

In both of these cases, it will be counted twice. The first case will be counted when $i = a$ and when $i = b$ . The second case will be counted when $i = b$ and when $i = c$ . Therefore, to compute the number of non-harmonic triples, we sum this calculation through all $i$ from $2$ to $n$ and divide it by $2$ .

Now all we have left to solve is to learn to count the number of coprimes to $i$ in the interval $[2; n]$ . Although this problem has already been mentioned, the above solution is not suitable here — it would require the factorization of each of the integers from $2$ to $n$ , and then iterating through all subsets of these primes.

A faster solution is possible with such modification of the sieve of Eratosthenes:

First, we find all numbers in the interval $[2; n]$ such that its simple factorization does not include a prime factor twice. We will also need to know, for these numbers, how many factors it includes.
- To do this we will maintain an array $d e g [i]$ to store the number of primes in the factorization of $i$ , and an array $g o o d [i]$ , to mark either if $i$ contains each factor at most once ( $g o o d [i] = 1$ ) or not ( $g o o d [i] = 0$ ). When iterating from $2$ to $n$ , if we reach a number that has $d e g$ equal to $0$ , then it is a prime and its $d e g$ is $1$ .
- During the sieve of Eratosthenes, we will iterate $i$ from $2$ to $n$ . When processing a prime number we go through all of its multiples and increase their $d e g []$ . If one of these multiples is multiple of the square of $i$ , then we can put $g o o d$ as false.
Second, we need to calculate the answer for all $i$ from $2$ to $n$ , i.e., the array $c n t []$ — the number of integers not coprime with $i$ .
- To do this, remember how the formula of inclusion-exclusion works — actually here we implement the same concept, but with inverted logic: we iterate over a component (a product of primes from the factorization) and add or subtract its term on the formula of inclusion-exclusion of each of its multiples.
- So, let's say we are processing a number $i$ such that $g o o d [i] = t r u e$ , i.e., it is involved in the formula of inclusion-exclusion. Iterate through all numbers that are multiples of $i$ , and either add or subtract $⌊ N / i ⌋$ from their $c n t []$ (the signal depends on $d e g [i]$ : if $d e g [i]$ is odd, then we must add, otherwise subtract).

Here's a C++ implementation:

int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];

long long solve() {
    memset (good, 1, sizeof good);
    memset (deg, 0, sizeof deg);
    memset (cnt, 0, sizeof cnt);

    long long ans_bad = 0;
    for (int i=2; i<=n; ++i) {
        if (good[i]) {
            if (deg[i] == 0)  deg[i] = 1;
            for (int j=1; i*j<=n; ++j) {
                if (j > 1 && deg[i] == 1)
                    if (j % i == 0)
                        good[i*j] = false;
                    else
                        ++deg[i*j];
                cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
            }
        }
        ans_bad += (cnt[i] - 1) * 1ll * (n-1 - cnt[i]);
    }

    return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}

The asymptotics of our solution is $O (n \log n)$ , as for almost every number up to $n$ we make $n / i$ iterations on the nested loop.

The number of permutations without fixed points (derangements)¶

Prove that the number of permutations of length $n$ without fixed points (i.e. no number $i$ is in position $i$ - also called a derangement) is equal to the following number:

n! - (\binom{n}{1}) \cdot (n - 1)! + (\binom{n}{2}) \cdot (n - 2)! - (\binom{n}{3}) \cdot (n - 3)! + \dots \pm (\binom{n}{n}) \cdot (n - n)!

and approximately equal to:

\frac{n!}{e}

(if you round this expression to the nearest whole number — you get exactly the number of permutations without fixed points)

Denote by $A_{k}$ the set of permutations of length $n$ with a fixed point at position $k$ ( $1 \leq k \leq n$ ) (i.e. element $k$ is at position $k$ ).

We now use the formula of inclusion-exclusion to count the number of permutations with at least one fixed point. For this we need to learn to count sizes of an intersection of sets $A_{i}$ , as follows:

\begin{array}{rcl} | A_{p} | & = & (n - 1)!, \\ | A_{p} \cap A_{q} | & = & (n - 2)!, \\ | A_{p} \cap A_{q} \cap A_{r} | & = & (n - 3)!, \\ \dots, \end{array}

because if we know that the number of fixed points is equal $x$ , then we know the position of $x$ elements of the permutation, and all other $(n - x)$ elements can be placed anywhere.

Substituting this into the formula of inclusion-exclusion, and given that the number of ways to choose a subset of size $x$ from the set of $n$ elements is equal to $(\binom{n}{x})$ , we obtain a formula for the number of permutations with at least one fixed point:

(\binom{n}{1}) \cdot (n - 1)! - (\binom{n}{2}) \cdot (n - 2)! + (\binom{n}{3}) \cdot (n - 3)! - \dots \pm (\binom{n}{n}) \cdot (n - n)!

Then the number of permutations without fixed points is equal to:

n! - (\binom{n}{1}) \cdot (n - 1)! + (\binom{n}{2}) \cdot (n - 2)! - (\binom{n}{3}) \cdot (n - 3)! + \dots \pm (\binom{n}{n}) \cdot (n - n)!

Simplifying this expression, we obtain exact and approximate expressions for the number of permutations without fixed points:

n! (1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \dots \pm \frac{1}{n!}) \approx \frac{n!}{e}

(because the sum in brackets are the first $n + 1$ terms of the expansion in Taylor series $e^{- 1}$ )

It is worth noting that a similar problem can be solved this way: when you need the fixed points were not among the $m$ first elements of permutations (and not among all, as we just solved). The formula obtained is as the given above accurate formula, but it will go up to the sum of $k$ , instead of $n$ .

Practice Problems¶

A list of tasks that can be solved using the principle of inclusions-exclusions:

Contributors:

gabrielsimoes (81.56%)
jakobkogler (5.64%)
adamant-pwn (4.34%)
turfaa (2.39%)
invincible0 (1.3%)
jxu (1.08%)
Kakalinn (0.65%)
lmiskiew (0.65%)
Morass (0.65%)
khan-shahnawaz (0.22%)
SiddharthEEE (0.22%)
rajatdiptabiswas (0.22%)
Salil03 (0.22%)
HurayraIIT (0.22%)
L1nkus (0.22%)
wikku (0.22%)
likecs (0.22%)