Delaunay triangulation and Voronoi diagram¶
Consider a set $\{p_i\}$ of points on the plane. A Voronoi diagram $V(\{p_i\})$ of $\{p_i\}$ is a partition of the plane into $n$ regions $V_i$, where $V_i = \{p\in\mathbb{R}^2;\ \rho(p, p_i) = \min\ \rho(p, p_k)\}$. The cells of the Voronoi diagram are polygons (possibly infinite). A Delaunay triangulation $D(\{p_i\})$ of $\{p_i\}$ is a triangulation where every point $p_i$ is outside or on the boundary of the circumcircle of each triangle $T \in D(\{p_i\})$.
There is a nasty degenerated case when the Voronoi diagram isn't connected and Delaunay triangulation doesn't exist. This case is when all points are collinear.
Properties¶
The Delaunay triangulation maximizes the minimum angle among all possible triangulations.
The Minimum Euclidean spanning tree of a point set is a subset of edges of its' Delaunay triangulation.
Duality¶
Suppose that $\{p_i\}$ is not collinear and among $\{p_i\}$ no four points lie on one circle. Then $V(\{p_i\})$ and $D(\{p_i\})$ are dual, so if we obtain one of them, we may obtain the other in $O(n)$. What to do if it's not the case? The collinear case may be processed easily. Otherwise, $V$ and $D'$ are dual, where $D'$ is obtained from $D$ by removing all the edges such that two triangles on this edge share the circumcircle.
Building Delaunay and Voronoi¶
Because of the duality, we only need a fast algorithm to compute only one of $V$ and $D$. We will describe how to build $D(\{p_i\})$ in $O(n\log n)$. The triangulation will be built via divide-and-conquer algorithm due to Guibas and Stolfi.
Quad-edge data structure¶
During the algorithm $D$ will be stored inside the quad-edge data structure. This structure is described in the picture:
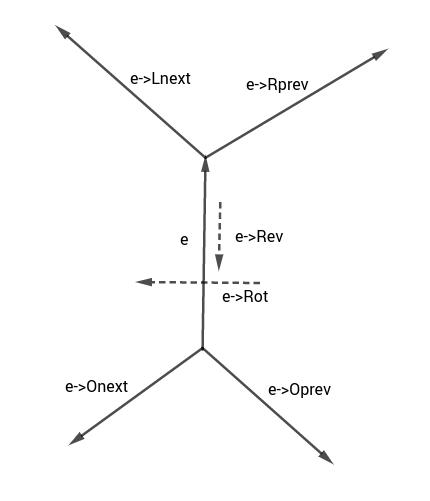
In the algorithm we will use the following functions on edges:
make_edge(a, b)
This function creates an isolated edge from pointato pointbtogether with its' reverse edge and both dual edges.splice(a, b)
This is a key function of the algorithm. It swapsa->Onextwithb->Onextanda->Onext->Rot->Onextwithb->Onext->Rot->Onext.delete_edge(e)
This function deletes e from the triangulation. To deletee, we may simply callsplice(e, e->Oprev)andsplice(e->Rev, e->Rev->Oprev).connect(a, b)
This function creates a new edgeefroma->Desttob->Orgin such a way thata,b,eall have the same left face. To do this, we calle = make_edge(a->Dest, b->Org),splice(e, a->Lnext)andsplice(e->Rev, b).
Algorithm¶
The algorithm will compute the triangulation and return two quad-edges: the counterclockwise convex hull edge out of the leftmost vertex and the clockwise convex hull edge out of the rightmost vertex.
Let's sort all points by x, and if $x_1 = x_2$ then by y. Let's solve the problem for some segment $(l, r)$ (initially $(l, r) = (0, n - 1)$). If $r - l + 1 = 2$, we will add an edge $(p[l], p[r])$ and return. If $r - l + 1 = 3$, we will firstly add the edges $(p[l], p[l + 1])$ and $(p[l + 1], p[r])$. We must also connect them using splice(a->Rev, b). Now we must close the triangle. Our next action will depend on the orientation of $p[l], p[l + 1], p[r]$. If they are collinear, we can't make a triangle, so we simply return (a, b->Rev). Otherwise, we create a new edge c by calling connect(b, a). If the points are oriented counter-clockwise, we return (a, b->Rev). Otherwise we return (c->Rev, c).
Now suppose that $r - l + 1 \ge 4$. Firstly, let's solve $L = (l, \frac{l + r}{2})$ and $R = (\frac{l + r}{2} + 1, r)$ recursively. Now we have to merge these triangulations into one triangulation. Note that our points are sorted, so while merging we will add edges from L to R (so-called cross edges) and remove some edges from L to L and from R to R.
What is the structure of the cross edges? All these edges must cross a line parallel to the y-axis and placed at the splitting x value. This establishes a linear ordering of the cross edges, so we can talk about successive cross edges, the bottom-most cross edge, etc. The algorithm will add the cross edges in ascending order. Note that any two adjacent cross edges will have a common endpoint, and the third side of the triangle they define goes from L to L or from R to R. Let's call the current cross edge the base. The successor of the base will either go from the left endpoint of the base to one of the R-neighbors of the right endpoint or vice versa.
Consider the circumcircle of base and the previous cross edge.
Suppose this circle is transformed into other circles having base as a chord but lying further into the Oy direction.
Our circle will go up for a while, but unless base is an upper tangent of L and R we will encounter a point belonging either to L or to R giving rise to a new triangle without any points in the circumcircle.
The new L-R edge of this triangle is the next cross edge added.
To do this efficiently, we compute two edges lcand and rcand so that lcand points to the first L point encountered in this process, and rcand points to the first R point.
Then we choose the one that would be encountered first. Initially base points to the lower tangent of L and R.
Implementation¶
Note that the implementation of the in_circle function is GCC-specific.
typedef long long ll;
bool ge(const ll& a, const ll& b) { return a >= b; }
bool le(const ll& a, const ll& b) { return a <= b; }
bool eq(const ll& a, const ll& b) { return a == b; }
bool gt(const ll& a, const ll& b) { return a > b; }
bool lt(const ll& a, const ll& b) { return a < b; }
int sgn(const ll& a) { return a >= 0 ? a ? 1 : 0 : -1; }
struct pt {
ll x, y;
pt() { }
pt(ll _x, ll _y) : x(_x), y(_y) { }
pt operator-(const pt& p) const {
return pt(x - p.x, y - p.y);
}
ll cross(const pt& p) const {
return x * p.y - y * p.x;
}
ll cross(const pt& a, const pt& b) const {
return (a - *this).cross(b - *this);
}
ll dot(const pt& p) const {
return x * p.x + y * p.y;
}
ll dot(const pt& a, const pt& b) const {
return (a - *this).dot(b - *this);
}
ll sqrLength() const {
return this->dot(*this);
}
bool operator==(const pt& p) const {
return eq(x, p.x) && eq(y, p.y);
}
};
const pt inf_pt = pt(1e18, 1e18);
struct QuadEdge {
pt origin;
QuadEdge* rot = nullptr;
QuadEdge* onext = nullptr;
bool used = false;
QuadEdge* rev() const {
return rot->rot;
}
QuadEdge* lnext() const {
return rot->rev()->onext->rot;
}
QuadEdge* oprev() const {
return rot->onext->rot;
}
pt dest() const {
return rev()->origin;
}
};
QuadEdge* make_edge(pt from, pt to) {
QuadEdge* e1 = new QuadEdge;
QuadEdge* e2 = new QuadEdge;
QuadEdge* e3 = new QuadEdge;
QuadEdge* e4 = new QuadEdge;
e1->origin = from;
e2->origin = to;
e3->origin = e4->origin = inf_pt;
e1->rot = e3;
e2->rot = e4;
e3->rot = e2;
e4->rot = e1;
e1->onext = e1;
e2->onext = e2;
e3->onext = e4;
e4->onext = e3;
return e1;
}
void splice(QuadEdge* a, QuadEdge* b) {
swap(a->onext->rot->onext, b->onext->rot->onext);
swap(a->onext, b->onext);
}
void delete_edge(QuadEdge* e) {
splice(e, e->oprev());
splice(e->rev(), e->rev()->oprev());
delete e->rev()->rot;
delete e->rev();
delete e->rot;
delete e;
}
QuadEdge* connect(QuadEdge* a, QuadEdge* b) {
QuadEdge* e = make_edge(a->dest(), b->origin);
splice(e, a->lnext());
splice(e->rev(), b);
return e;
}
bool left_of(pt p, QuadEdge* e) {
return gt(p.cross(e->origin, e->dest()), 0);
}
bool right_of(pt p, QuadEdge* e) {
return lt(p.cross(e->origin, e->dest()), 0);
}
template <class T>
T det3(T a1, T a2, T a3, T b1, T b2, T b3, T c1, T c2, T c3) {
return a1 * (b2 * c3 - c2 * b3) - a2 * (b1 * c3 - c1 * b3) +
a3 * (b1 * c2 - c1 * b2);
}
bool in_circle(pt a, pt b, pt c, pt d) {
// If there is __int128, calculate directly.
// Otherwise, calculate angles.
#if defined(__LP64__) || defined(_WIN64)
__int128 det = -det3<__int128>(b.x, b.y, b.sqrLength(), c.x, c.y,
c.sqrLength(), d.x, d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), c.x, c.y, c.sqrLength(), d.x,
d.y, d.sqrLength());
det -= det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), d.x,
d.y, d.sqrLength());
det += det3<__int128>(a.x, a.y, a.sqrLength(), b.x, b.y, b.sqrLength(), c.x,
c.y, c.sqrLength());
return det > 0;
#else
auto ang = [](pt l, pt mid, pt r) {
ll x = mid.dot(l, r);
ll y = mid.cross(l, r);
long double res = atan2((long double)x, (long double)y);
return res;
};
long double kek = ang(a, b, c) + ang(c, d, a) - ang(b, c, d) - ang(d, a, b);
if (kek > 1e-8)
return true;
else
return false;
#endif
}
pair<QuadEdge*, QuadEdge*> build_tr(int l, int r, vector<pt>& p) {
if (r - l + 1 == 2) {
QuadEdge* res = make_edge(p[l], p[r]);
return make_pair(res, res->rev());
}
if (r - l + 1 == 3) {
QuadEdge *a = make_edge(p[l], p[l + 1]), *b = make_edge(p[l + 1], p[r]);
splice(a->rev(), b);
int sg = sgn(p[l].cross(p[l + 1], p[r]));
if (sg == 0)
return make_pair(a, b->rev());
QuadEdge* c = connect(b, a);
if (sg == 1)
return make_pair(a, b->rev());
else
return make_pair(c->rev(), c);
}
int mid = (l + r) / 2;
QuadEdge *ldo, *ldi, *rdo, *rdi;
tie(ldo, ldi) = build_tr(l, mid, p);
tie(rdi, rdo) = build_tr(mid + 1, r, p);
while (true) {
if (left_of(rdi->origin, ldi)) {
ldi = ldi->lnext();
continue;
}
if (right_of(ldi->origin, rdi)) {
rdi = rdi->rev()->onext;
continue;
}
break;
}
QuadEdge* basel = connect(rdi->rev(), ldi);
auto valid = [&basel](QuadEdge* e) { return right_of(e->dest(), basel); };
if (ldi->origin == ldo->origin)
ldo = basel->rev();
if (rdi->origin == rdo->origin)
rdo = basel;
while (true) {
QuadEdge* lcand = basel->rev()->onext;
if (valid(lcand)) {
while (in_circle(basel->dest(), basel->origin, lcand->dest(),
lcand->onext->dest())) {
QuadEdge* t = lcand->onext;
delete_edge(lcand);
lcand = t;
}
}
QuadEdge* rcand = basel->oprev();
if (valid(rcand)) {
while (in_circle(basel->dest(), basel->origin, rcand->dest(),
rcand->oprev()->dest())) {
QuadEdge* t = rcand->oprev();
delete_edge(rcand);
rcand = t;
}
}
if (!valid(lcand) && !valid(rcand))
break;
if (!valid(lcand) ||
(valid(rcand) && in_circle(lcand->dest(), lcand->origin,
rcand->origin, rcand->dest())))
basel = connect(rcand, basel->rev());
else
basel = connect(basel->rev(), lcand->rev());
}
return make_pair(ldo, rdo);
}
vector<tuple<pt, pt, pt>> delaunay(vector<pt> p) {
sort(p.begin(), p.end(), [](const pt& a, const pt& b) {
return lt(a.x, b.x) || (eq(a.x, b.x) && lt(a.y, b.y));
});
auto res = build_tr(0, (int)p.size() - 1, p);
QuadEdge* e = res.first;
vector<QuadEdge*> edges = {e};
while (lt(e->onext->dest().cross(e->dest(), e->origin), 0))
e = e->onext;
auto add = [&p, &e, &edges]() {
QuadEdge* curr = e;
do {
curr->used = true;
p.push_back(curr->origin);
edges.push_back(curr->rev());
curr = curr->lnext();
} while (curr != e);
};
add();
p.clear();
int kek = 0;
while (kek < (int)edges.size()) {
if (!(e = edges[kek++])->used)
add();
}
vector<tuple<pt, pt, pt>> ans;
for (int i = 0; i < (int)p.size(); i += 3) {
ans.push_back(make_tuple(p[i], p[i + 1], p[i + 2]));
}
return ans;
}