Second Best Minimum Spanning Tree¶
A Minimum Spanning Tree $T$ is a tree for the given graph $G$ which spans over all vertices of the given graph and has the minimum weight sum of all the edges, from all the possible spanning trees. A second best MST $T'$ is a spanning tree, that has the second minimum weight sum of all the edges, from all the possible spanning trees of the graph $G$.
Observation¶
Let $T$ be the Minimum Spanning Tree of a graph $G$. It can be observed, that the second best Minimum Spanning Tree differs from $T$ by only one edge replacement. (For a proof of this statement refer to problem 23-1 here).
So we need to find an edge $e_{new}$ which is in not in $T$, and replace it with an edge in $T$ (let it be $e_{old}$) such that the new graph $T' = (T \cup \{e_{new}\}) \setminus \{e_{old}\}$ is a spanning tree and the weight difference ($e_{new} - e_{old}$) is minimum.
Using Kruskal's Algorithm¶
We can use Kruskal's algorithm to find the MST first, and then just try to remove a single edge from it and replace it with another.
- Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
- For each edge in the MST (we will have $V-1$ edges in it) temporarily exclude it from the edge list so that it cannot be chosen.
- Then, again try to find a MST in $O(E)$ using the remaining edges.
- Do this for all the edges in MST, and take the best of all.
Note: we don’t need to sort the edges again in for Step 3.
So, the overall time complexity will be $O(E \log V + E + V E)$ = $O(V E)$.
Modeling into a Lowest Common Ancestor (LCA) problem¶
In the previous approach we tried all possibilities of removing one edge of the MST. Here we will do the exact opposite. We try to add every edge that is not already in the MST.
- Sort the edges in $O(E \log E)$, then find a MST using Kruskal in $O(E)$.
- For each edge $e$ not already in the MST, temporarily add it to the MST, creating a cycle. The cycle will pass through the LCA.
- Find the edge $k$ with maximal weight in the cycle that is not equal to $e$, by following the parents of the nodes of edge $e$, up to the LCA.
- Remove $k$ temporarily, creating a new spanning tree.
- Compute the weight difference $\delta = weight(e) - weight(k)$, and remember it together with the changed edge.
- Repeat step 2 for all other edges, and return the spanning tree with the smallest weight difference to the MST.
The time complexity of the algorithm depends on how we compute the $k$s, which are the maximum weight edges in step 2 of this algorithm. One way to compute them efficiently in $O(E \log V)$ is to transform the problem into a Lowest Common Ancestor (LCA) problem.
We will preprocess the LCA by rooting the MST and will also compute the maximum edge weights for each node on the paths to their ancestors. This can be done using Binary Lifting for LCA.
The final time complexity of this approach is $O(E \log V)$.
For example:
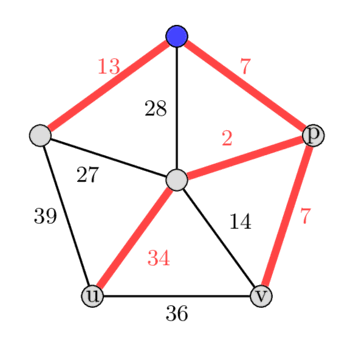
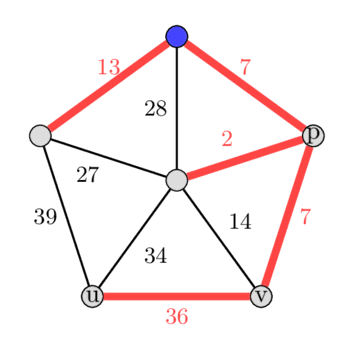
*In the image left is the MST and right is the second best MST.*
In the given graph suppose we root the MST at the blue vertex on the top, and then run our algorithm by start picking the edges not in MST. Let the edge picked first be the edge $(u, v)$ with weight 36. Adding this edge to the tree forms a cycle 36 - 7 - 2 - 34.
Now we will find the maximum weight edge in this cycle by finding the $\text{LCA}(u, v) = p$. We compute the maximum weight edge on the paths from $u$ to $p$ and from $v$ to $p$. Note: the $\text{LCA}(u, v)$ can also be equal to $u$ or $v$ in some case. In this example we will get the edge with weight 34 as maximum edge weight in the cycle. By removing the edge we get a new spanning tree, that has a weight difference of only 2.
After doing this also with all other edges that are not part of the initial MST, we can see that this spanning tree was also the second best spanning tree overall. Choosing the edge with weight 14 will increase the weight of the tree by 7, choosing the edge with weight 27 increases it by 14, choosing the edge with weight 28 increases it by 21, and choosing the edge with weight 39 will increase the tree by 5.
Implementation¶
struct edge {
int s, e, w, id;
bool operator<(const struct edge& other) { return w < other.w; }
};
typedef struct edge Edge;
const int N = 2e5 + 5;
long long res = 0, ans = 1e18;
int n, m, a, b, w, id, l = 21;
vector<Edge> edges;
vector<int> h(N, 0), parent(N, -1), size(N, 0), present(N, 0);
vector<vector<pair<int, int>>> adj(N), dp(N, vector<pair<int, int>>(l));
vector<vector<int>> up(N, vector<int>(l, -1));
pair<int, int> combine(pair<int, int> a, pair<int, int> b) {
vector<int> v = {a.first, a.second, b.first, b.second};
int topTwo = -3, topOne = -2;
for (int c : v) {
if (c > topOne) {
topTwo = topOne;
topOne = c;
} else if (c > topTwo && c < topOne) {
topTwo = c;
}
}
return {topOne, topTwo};
}
void dfs(int u, int par, int d) {
h[u] = 1 + h[par];
up[u][0] = par;
dp[u][0] = {d, -1};
for (auto v : adj[u]) {
if (v.first != par) {
dfs(v.first, u, v.second);
}
}
}
pair<int, int> lca(int u, int v) {
pair<int, int> ans = {-2, -3};
if (h[u] < h[v]) {
swap(u, v);
}
for (int i = l - 1; i >= 0; i--) {
if (h[u] - h[v] >= (1 << i)) {
ans = combine(ans, dp[u][i]);
u = up[u][i];
}
}
if (u == v) {
return ans;
}
for (int i = l - 1; i >= 0; i--) {
if (up[u][i] != -1 && up[v][i] != -1 && up[u][i] != up[v][i]) {
ans = combine(ans, combine(dp[u][i], dp[v][i]));
u = up[u][i];
v = up[v][i];
}
}
ans = combine(ans, combine(dp[u][0], dp[v][0]));
return ans;
}
int main(void) {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
parent[i] = i;
size[i] = 1;
}
for (int i = 1; i <= m; i++) {
cin >> a >> b >> w; // 1-indexed
edges.push_back({a, b, w, i - 1});
}
sort(edges.begin(), edges.end());
for (int i = 0; i <= m - 1; i++) {
a = edges[i].s;
b = edges[i].e;
w = edges[i].w;
id = edges[i].id;
if (unite_set(a, b)) {
adj[a].emplace_back(b, w);
adj[b].emplace_back(a, w);
present[id] = 1;
res += w;
}
}
dfs(1, 0, 0);
for (int i = 1; i <= l - 1; i++) {
for (int j = 1; j <= n; ++j) {
if (up[j][i - 1] != -1) {
int v = up[j][i - 1];
up[j][i] = up[v][i - 1];
dp[j][i] = combine(dp[j][i - 1], dp[v][i - 1]);
}
}
}
for (int i = 0; i <= m - 1; i++) {
id = edges[i].id;
w = edges[i].w;
if (!present[id]) {
auto rem = lca(edges[i].s, edges[i].e);
if (rem.first != w) {
if (ans > res + w - rem.first) {
ans = res + w - rem.first;
}
} else if (rem.second != -1) {
if (ans > res + w - rem.second) {
ans = res + w - rem.second;
}
}
}
}
cout << ans << "\n";
return 0;
}
References¶
- Competitive Programming-3, by Steven Halim
- web.mit.edu